In 1931 kwam professor Georges Lemaître van de universiteit van Leuven met het idee dat ooit, ergens tussen 5 en 20 miljard jaar geleden, het heelal ontstond als een oeratoom met een oneindig dichte massa. Dit idee is nu algemeen aanvaard, men noemt het de oerknal, en die zou plaatsgevonden hebben voor 13,7 miljard jaar.
De stad Leuven wil niet wachten tot de honderdste verjaardag om die aankondiging te vieren. Al in 2021 vieren we 90 jaar oerknal met een culturele big bang. En bij die gelegenheid wil ik vertellen hoe en waarom wetenschappers op dat idee gekomen zijn.
Ik begin het verhaal rond het jaar 300 voor Christus.
In die tijd verzamelde de Griekse wiskundige Euclides van Alexandrië de toenmalige kennis over meetkunde in een boek dat gedurende duizenden jaren als model zou dienen voor wiskundigen. Hij begon met enkele definities: hierover zal het gaan. Daarna volgden een beperkt aantal basisbeweringen: laten we dit gewoon aanvaarden. En daarna kwam een onbeperkt aantal stellingen (iedereen mag er de zijne aan toevoegen), waarvan men bewijst dat ze logisch volgen uit de definities en de basisbeweringen.
Maar zoals gezegd, het boek ging niet over wiskunde, maar over meetkunde: over de ruimte waarin we leven, over de vormen en groottes in die ruimte. Dat is natuurkunde. In de natuurkunde gebruikt men dikwijls wiskundige methodes.
Dat Euclides niet dacht te schrijven over zuivere wiskunde, kunnen we afleiden uit het onderscheid dat hij maakte tussen zijn basisbeweringen. In de wiskunde is een basisbewering een basisbewering. Een axioma noemt men dat. Euclides gaf enkele axiomas, die voor hem vanzelfsprekend waren. Door twee verschillende punten loopt een en slechts een rechte. Niemand zal dat tegenspreken. Maar daarnaast stelde hij ook een postulaat voor, volgens hem een bewering die waarschijnlijk waar is, maar waarover men toch kan twijfelen. Door een punt buiten een rechte gaat er in hetzelfde vlak een en slechts een evenwijdige rechte. Laten we dat veronderstellen, en zien waar het ons brengt.
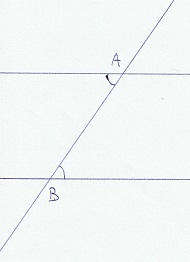We tekenen twee evenwijdige rechten, en daardoor nog een derde rechte. We
zien onmiddellijk dat de hoeken in A gelijk zijn aan de hoeken in B. De kleine hoek in A kan niet groter of kleiner zijn dan deze in B, want de twee
punten en rechten bevinden zich in dezelfde positie ten opzichte van elkaar, en de evenwijdige rechten zijn uniek.
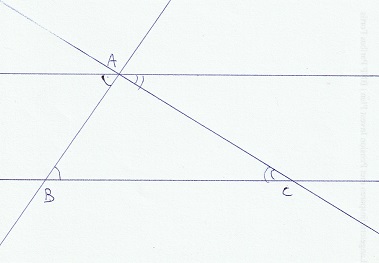Als we nu een andere rechte toevoegen door A, dan zullen de aangeduide
hoeken in A en C natuurlijk ook gelijk zijn. Onder het punt A zien we nu dat de som van de hoeken van een driehoek gelijk is aan 180°.
Daaruit volgt dat er gelijkvormige driehoeken bestaan die niet noodzakelijk even groot zijn: copieer gewoon twee hoeken van de eerste driehoek (de afstand heeft geen belang), en de derde hoek van de nieuwe driehoek zal gelijk zijn aan de derde hoek van de eerste.
Uit de eigenschappen van gelijkvormige driehoeken volgt praktisch heel de Euclidische meetkunde: alles wat gaat over lengtes. Het postulaat vanµ
Euclides is heel belangrijk om de ruimte te kennen waarin we leven.
Maar toch kunnen we ons gemakkelijk een andere ruimte inbeelden, misschien niet in drie dimensies, maar in twee. Denk aan tweedimensionale wezentjes, die leven op een bolvormig oppervlak. Op een bol is de som van de hoeken van een driehoek meer dan 180°. Maar onze tweedimensionaaltjes kennen maar een klein deel van hun wereld: zij kennen Leuven op de oppervlakte van de aarde. In Leuven is de som van de hoeken van een driehoek 180°, eigenlijk iets meer, maar het verschil is onmeetbaar klein. De wereld lijkt Euclidisch.
Dit is nu echte wetenschap: misschien niet helemaal waar, nooit helemaal zeker, maar wel nauwkeurig juist in het deel van de wereld dat we kennen.
In de 16e en 17e eeuw betudeerden verschillende wetenschappers bewegingen. Johannes Kepler beschreef de beweging van de planeten. Galileo Galilei bestudeerde bewegingen op aarde en de invloed van de zwaartekracht. Isaac Newton vatte de bevindingen van Gelilei samen in een meer wiskundig systeem, en verklaarde de wetten van Kepler over de beweging van planeten als een gevolg van dezelfde zwaartekracht die Galilei beschreef op aarde.
Twee ideeën uit die tijd zijn belangrijk voor mijn verhaal.
Wel bestaan er enkele speciale waarnemers: inertiële waarnemers zijn waarnemers waarop geen netto kracht inwerkt. Ten opzichte van elkaar bewegen deze waarnemers niet, of ze bewegen in rechte lijn met een constante snelheid.
Dat deze twee massa's aspecten zijn van dezelfde realiteit, leidde hij af uit verschillende feiten, maar vooral uit een experiment toegeschreven aan Galilei, die twee kogels, de ene van lood, de andere van ijzer, liet vallen van een hoge toren; de kogels bereikten gelijktijdig de grond. Dit experiment werd later nog dikwijls overgedaan met voorwerpen uit verschillende materialen en in verschillende vormen, zelfs met een pluim en een kogel in een luchtledige buis, en altijd met hetzelfde resultaat.
In de 19e eeuw experimenteerde Michael Faraday met elektriciteit en magnetisme en de wisselwerking tussen beide. James Clerk Maxwell werkte aan de hand van zijn resultaten een theorie van het elektromagnetisme uit. Uit deze theorie volgde dat er elektromagnetische golven moeten bestaan, die in vacuum een vaste snelheid hebben die kan berekend worden uit de resultaten van Faraday. Deze snelheid is gelijk aan de al vroeger gemeten snelheid van het licht. Daarom heeft men onmiddellijk verondersteld, en later ook bewezen, dat licht een elektromagnetische golf is.
Maar een golf in vacuum, heeft dat wel een snelheid? Ten opzichte van wat? Ten opzichte van de instrumenten van Faraday in een Londens laboratorium, dat lijkt niet zo geloofwaardig als antwoord. Het eerste idee was dat die golven bewegen door de ether, een speciale stof die geen invloed heeft op andere stoffen, en enkel dient om lichtgolven te dragen.
Goed, maar die ether moet toch zelf ook een plaats hebben. Aangezien de aarde met een snelheid van 30 km/s rond de zon draait, lijkt het erop dat de aarde beweegt ten opzichte van de ether. Licht dat beweegt in dezelfde richting als de aarde moet trager zijn ten opzichte van de aarde, dan licht dat uit de tegenovergestelde richting komt. Experimenteel vond men echter geen enkel verschil.
In 1905 stelde Albert Einstein een oplossing voor zonder ether. Laten we gewoon aanvaarden dat de lichtsnelheid dezelfde is voor elke waarnemer: we wijzigen de relativiteitstheorie van Galilei.
 |
 |
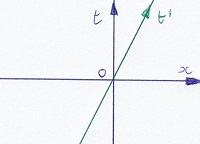
Bekijk dit diagram. Horizontaal teken ik de ruimte, vertikaal de tijd. Van de ruimte zien we alleen de x-coordinaat, maar alle relevante bewegingen zullen plaatshebben in de positieve of negatieve x-richting. Punten in dergelijk diagram noemen we gebeurtenissen of eventen, omdat ze bepaald zijn in plaats en in tijd. Het event O is onze referentie: daar zijn x en t gelijk aan nul. Het diagram toont de eventen vanuit het oogpunt van de vaste grond. In event O komt een trein voorbij met constante snelheid. De groene lijn toont eventen gebonden aan een vast punt in de trein.
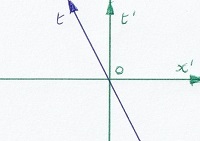
Daaronder zien we dezelfde eventen, maar nu gezien vanuit de trein. In beide diagrammen verbinden vertikale lijnen eventen op eenzelfde plaats. In het eerste diagram gaat de trein naar rechts, in het tweede gaat de vaste grond naar links.
Galilei zegt niets over de tijd, maar impliciet veronderstelt hij dat de tijd gelijk is voor iedereen. Horizontale lijnen blijven horizontaal in elk diagram.
 |
 |
Maar als de lichtsnelheid voor iedereen gelijk is, is dat niet mogelijk. In het rood voeg ik twee lichtstralen toe vanuit O: een naar links, een naar rechts. De eenheden voor lengte en tijd zijn zo gekozen dat de lichtsnelheid gelijk is aan 1: één lichtseconde per seconde. Onze trein rijdt heel snel. Voor een tragere trein zou de theorie van Einstein bijna niets veranderen.
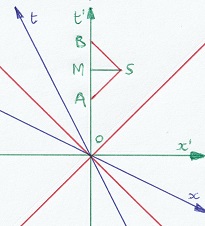
Wat verandert er nu? In de trein (onderste diagram), in event A, vertrekt een lichtstraal naar een spiegel, in B komt ze terug. De spiegel bevindt zich op de trein, dus blijft op een vaste afstand. Het spiegelen, event S, gebeurt gelijktijdig met M, het event halfweg tussen A en B.
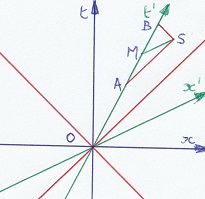
Boven staan dezelfde eventen, maar gezien vanaf de vaste grond. A en B bevinden zich op de lijn die de beweging van de trein weergeeft. M is het midden tussen A en B. Het licht heeft een constante snelheid, dus we kunnen tekenen hoe de lichtstraal vertrekt, en hoe ze terugkeert. Event S is waar de twee lichtstralen elkaar ontmoeten. Gezien vanuit de trein was dit gelijktijdig met M, maar vanaf de vaste grond zijn de eventen duidelijk niet gelijktijdig. Niet alleen de plaats is relatief, maar ook de tijd.
Nemen we er twee ruimtelijke coordinaten bij: y en z, beide loodrecht op x en op elkaar. De eenheid van tijd blijft gelijk aan de eenheid van afstand,
zodat de lichtsnelheid gelijk blijft aan 1. Men kan bewijzen dat voor elk event P(x, y, z, t) de waarde van x2
+ y2 + z2 - t2 gelijk is voor alle waarnemers. We noemen dit het interval tussen O(0, 0, 0, 0) en P. Voor
eventen op een lichtstraal uit O, is het interval nul. Als het interval positief is, is het gelijk aan het kwadraat van de eigen afstand, dat is de
afstand zoals die gemeten zou worden door iemand voor wie de eventen gelijktijdig zijn. Is het negatief, dan is het gelijk aan min het kwadraat van
de eigen tijd, het tijdverschil gemeten door iemand die meereist, zodat P voor hem op dezelfde plaats blijft als O.
Deze formule, samen met enkele veronderstellingen die ervoor moeten zorgen dat bij lage snelheid de al gekende natuurwetten geldig blijven, vormt de basis van wat we nu de Speciale Relativiteitstheorie noemen, speciaal omdat ze alleen het speciaal geval behandelt van waarnemers met een constante snelheid.
Ik ga daar niet verder op in. Eén resultaat hebben we wel nog nodig voor het vervolg. Als de formule van Newton waarin de inertiële massa voorkomt, geldig moet blijven, dan zal die massa afhankelijk zijn van de snelheid van het voorwerp: hoe groter de snelheid, hoe groter de massa. De rustmassa is
de massa gemeten door een meereizende waarnemer. Licht heeft geen rustmassa, want zijn snelheid is dezelfde voor alle waarnemers: er bestaat geen
waarnemer voor wie die snelheid nul is. En een voorwerp waarvan de rustmassa niet nul is, kan nooit versnellen tot de snelheid van het licht, want
daarvoor zou een oneindig grote kracht nodig zijn.
De Algemene Relativiteitstheorie, gepubliceerd in 1916, is ingewikkelder. Ik zal ze uitleggen, maar eerst moet ik iets zeggen over auto's. Een auto is een eenvoudig voorwerp, maar kijk niet naar de motor, het stuur of de pedalen. Hetzelfde geldt voor de relativiteit: ik toon u de vier wielen.
De Speciale Relativiteit zegt niets over wat een waarnemer ziet wiens snelheid niet constant is. Ook de zwaartekracht zorgde voor problemen.
Terwijl hij daarover nadacht, herinnerde Einstein zich het experiment van Galilei met de vallende voorwerpen. Twee voorwerpen in vrije val in een zwaartekrachtsveld bewegen niet ten opzichte van elkaar. Moeten we daarom niet veronderstellen dat juist die vallende voorwerpen de inertiële waarnemers zijn voor wie de regels van de Speciale Relativiteit gelden? Laten we veronderstellen dat de ruimtetijd zodanig verbogen wordt door de zwaartekracht, dat vallende voorwerpen uit hun eigen oogpunt geen enkele kracht ondervinden, en dat ze vallende voorwerpen in hun omgeving zien bewegen in een rechte lijn.
De oplossing voor het probleem zat dus in een gekromde meetkunde, zoals de niet-euclidische meetkundes die Bernard Riemann wiskundig bestudeerd had in het begin van de 19e eeuw. De meetkunde van de Algemene Relativiteit wordt pseudo-riemanns genoemd, omwille van de speciale afstandsformule met positieve en negatieve intervallen, maar veel technieken van Riemann blijven erop toepasbaar.
Een tweedimensionale Riemannmeetkunde kunnen we ons gemakkelijk voorstellen. Denk een het oppervlak van een berglandschap, met bergen en dalen, grotten en uitsteeksels, maar wel glad in al zijn punten. Dit betekent dat elk punt een omgeving heeft die bijna euclidisch is: met rechte lijntjes, driehoeken van 180°, en de gekende afstanden tussen naburige punten. Alleen als we een grotere omgeving bekijken, zullen we misschien ontdekken dat de ruimte gebogen is: de som van de hoeken van een grote driehoek is niet juist 180°, maar iets meer (zoals op een bol) of minder (zoals op een zadeloppervlak).
Rechten bestaan niet in een dergelijke ruimte, of tenminste men spreekt niet over rechten. Volgens Euclides is een rechte volledig bepaald door twee van haar punten. Door twee verschillende punten gaat een en slechts een rechte. Dergelijke rechten bestaan niet. Wel bestaan er geodetische lijnen of geodeten: lijnen die recht zijn in de euclidische omgeving van elk punt. Vanuit een punt gaat de lijn recht naar een naburig punt, van de buur gaat ze recht door naar een overbuur, en zo voort.
 |
 |
Een geodetische lijn is de kortste weg tussen twee van haar punten, in die zin dat een kleine verandering eraan ze alleen langer kan maken. Wel is het mogelijk dat een heel andere geodeet, met een andere lengte, door dezelfde twee punten gaat.
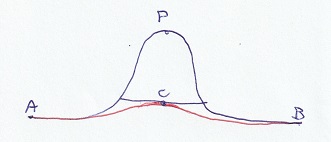
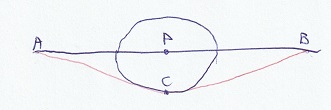
Kijk naar deze berg. Dezelfde punten en lijnen zijn twee keer getekend, gezien vanuit verschillende perspectieven. Boven zien we dat het om een berg gaat, onderaan dat de berg rond is. De kortste weg van A naar P en de kortste weg van P naar B zijn allebei geodeten. In het punt P liggen ze in elkaars verlengde. De hele weg van A naar B door P is dus geodetisch. Maar een andere geodeet van A naar B, door C, is korter.
Een dergelijke ruimte, maar vierdimensionaal met een aparte behandeling van de tijd, is wat Einstein voorstelde in zijn Algemene Relativiteitstheorie. Aanwezige massa's bepalen de vorm van de ruimte, en een vallend voorwerp beweegt in deze ruimte langs een geodetische lijn.
Het is iets ingewikkelder. In de Speciale Relativiteit hangt de massa van een voorwerp af van zijn snelheid. Verschillende waarnemers zien een
verschillende massa. Wel kan men de massa van voorwerp dat in rechte lijn beweegt voorstellen als een vector. Een vector is een wiskundig object dat een
realiteit voorstelt die verschillende waarnemers zullen beschrijven met verschillende maten. Bijvoorbeeld de snelheid van een voorwerp in een
driedimensionale ruimte: er zijn snelheden in richting x, y, en z. Kies andere richtingen voor x, y en z, en de drie snelheden gaan anders zijn, maar
dezelfde beweging weergeven. In de Speciale Relativiteit bestaat de vierdimensionale vector die in de plaats komt van de massa, uit de massa zoals
gezien door een bepaalde waarnemer (maal de lichtsnelheid) en de hoeveelheid van beweging (massa maal snelheid) in de drie ruimtelijke richtingen.
In een gekromde ruimtetijd is zelfs dat niet mogelijk, want punten van hetzelfde voorwerp hebben niet dezelfde snelheid ten opzichte van de waarnemer. Denk aan een draaiend wiel. Wat is de massa van zo een voorwerp? Men kan wel spreken over afzonderlijke punten van het voorwerp, en de plaatselijke massa beschrijven als een tensor, een soort veralgemening van een vector, waarvan de maten afhangen van meer dan een richting tegelijk. Die tensor bestaat in elk event, en bepaalt voor elke waarnemer enkele grootheden, die ik hier opsom in volgorde van belangrijkheid, in de veronderstelling dat alle snelheden klein zijn.
Die tensor van dichtheid, stroom en spanning bepaalt de plaatselijke kromming van de ruimte, op zo een manier we dat bij lage snelheid de bewegingen terugvinden die voorspeld werden door de wetten van Newton.
Is dat geen mooi resultaat? Met een berekening ingewikkelder dan die van Newton, vinden we hetzelfde resultaat. Maar de berekening van Newton geldt alleen bij lage snelheden en spanningen. Astronomen zochten al lang naar een uitleg voor iets raars in de omloop van Mercurius. Planeten beïnvloeden elkaar. Dat maakt hun omloop ingewikkelder, maar bij een gedetailleerde berekening van de banen van de planeten vond men meestal een resultaat in overeenstemming met de waarnemingen. Alleen bij Mercurius bleef er een onverklaarde onregelmatigheid, en die was groter dan de onzekerheid over de waarnemingen zelf. Maar Mercurius is de planeet het dichtst bij de zon, die dus ook het snelst beweegt, en waarvoor het verschil tussen Einstein en Newton het grootst moest zijn. De berekening van Einstein gaf bijna exact het resultaat dat de astronomen zochten.
Einstein verklaarde al gedane waarnemingen, maar hij voorspelde ook een nieuwe waarneming. Als de zwaartekracht de vorm van de ruimtetijd bepaalt, dan beïnvloedt dat niet alleen planeten, maar ook het licht. Ook licht moet een geodetische weg volgen, want een rechte weg bestaat niet. Licht dat langs de zon scheert moet voor ons afgebogen worden. Sterren waarvan de nachtelijke positie aan de hemel goed gekend is, moeten een iets andere positie krijgen als de zon vlakbij lijkt. Dat had men nog nooit opgemerkt, omdat men alleen 's nachts naar de sterren kijkt. Overdag is dat alleen mogelijk tijdens een zonsverduistering. Tijdens een verduistering in 1919 werd er wel naar de sterren gekeken, en die stonden op de plaats waar Einstein ze verwacht had.
Newton had zich al de vraag gesteld: als de zwaartekracht universeel is, moeten de sterren toch ook elkaar aantrekken. Moet het heelal dan niet krimpen? Zijn antwoord was, dat dat geen probleem moest zijn in een oneindig groot heelal: de zon wordt naar hier en naar daar getrokken, maar tegengestelde krachten heffen elkaar op: de zon zal niet bewegen, en de sterren ook niet.
|
Eigenlijk was het de Russische natuurwetenschapper Aleksander Friedmann die Einstein hierop attent maakte in 1922. Maar aangezien hij stierf in 1925, en zijn artikels tot dan toe geen aandacht trokken buiten de Sovjetunie, zal hij hier verder geen rol spelen. |
Einstein bekeek de vraag opnieuw. In de Algemene Relativiteit is zwaartekracht geen echte kracht, maar een kromming in de ruimte. Geodetische levenslijnen die op een bepaald ogenblik evenwijdig lijken, zoals meridianen aan de evenaar, kunnen verderop toch samenkomen. Dingen die niet bewegen in de ruimte, zullen samenkomen door de kromming die ze veroorzaken in de ruimtetijd. De invloed van verdergelegen objecten zal daar niets aan veranderen. Een onbeweeglijk heelal zal krimpen, of het oneindig is of niet. Het verschil is, dat in de wereld van Newton, het heelal maar kan krimpen als alle sterren naar een centraal punt bewegen. In die van Einstein is een centraal punt niet nodig. Vanuit haar eigen gezichtspunt kan elke ster op haar plaats blijven, maar de andere sterren komen dichterbij.
Als het heelal aan het uitdijen is, zal die uitdijing nog even voortduren. Of dat eeuwig blijft duren, hangt af van de snelheid van de uitdijing en van de dichtheid van het heelal op dit ogenblik. Maar omdat in die tijd, begin twintigste eeuw, de meeste astronomen dachten dat de dichtheid van het heelal niet verandert, paste Einstein zijn oorspronkelijke formule van de Algemene Relativiteit aan, door toevoeging van een op dat moment nog onbepaalde kosmologische constante. Die constante moest werken als een negatieve kromming van de lege ruite. Massa's trekken elkaar aan, maar als de lege ruimte tussenin groot genoeg is, stoot die lege ruimte hen af.
Maar ook de sterrenkunde stond niet stil.
In de negentiende eeuw had men al veel afstanden naar hemellichamen gemeten, door perspectieven te vergelijken. Voor planeten werd het uitzicht vergeleken dat men had vanuit verschillende observatoria. Voor sterren vergeleek men foto's gemaakt met dezelfde telescoop, maar vanuit verschillende posities van de aarde in haar omloop rond de zon. Zo kende men al de afstanden naar veel sterren in onze omgeving.
In de twintigste eeuw begon men een biologische methode te gebruiken om toch minstens een idee te hebben van grotere afstanden. Als een bioloog een olifant ziet, herkent hij onmiddellijk zijn vorm, en uit de schijnbare grootte kan hij een afstand afleiden. Herkent hij een vlieg, dan wordt de geschatte afstand kleiner. Ook onder de sterren zijn er dergelijke "dieren" waarvan kenners de ware grootte kennen. Zo kon men bewijzen dat verschillende zogenaamde sterrennevels veel verder van ons af staan dan de bekende sterren, en dat het eigenlijk sterrenstelsels zijn vergelijkbaar met onze Melkweg. In het Nederlands noemen we die nu melkwegstelsels, in veel andere talen gebruikt men een woord afgeleid uit γαλαξίας (galaksias), de Griekse naam van de Melkweg.
In de jaren 1920 mat Edwin Hubble de afstand en de roodverschuiving van een twintigtal melkwegen. Roodverschuiving is een eigenschap van het spectrum van licht. Het licht van sterren en melkwegen toont, als men zijn kleuren uitsplitst, een herkenbaar patroon, maar dat patroon kan verschoven zijn naar grotere of kleinere frekwenties naargelang de beweging van de ster. Verschuiving naar het blauw (grotere frekwenties) betekent dat de ster ons nadert. Maar bijna alle melkwegstelsels hebben een positieve roodverschuiving, wat betekent dat ze zich van ons verwijderen. Hubble stelde vast dat de verste sterrenstelsels de grootste roodverschuiving hebben.
Hoewel Hubble de vaststelling deed, is het Lemaître die als eerste met de besluiten naar buiten kwam, omdat hij zich uit theoretische overwegingen voldoende zeker voelde om dat te doen. De Algemene Relativiteit had hem geleerd dat als het heelal nu aan het uitdijen is, het vroeger ook al aan het uitdijen was, en het begin van die uitdijing moest een event zijn met oneindige dichtheid, op een eindige tijd voor vandaag. Dat is zo voor elke mogelijke waarde van de kosmologische constante.
Toen Lemaître voor het eerst met Einstein sprak over deze theorie van het oneindig dichte oeratoom (later zou hij spreken van het kosmisch ei), antwoordde Einstein onmiddellijk "Uw berekening is juist, maar uw natuurkunde trekt op niets." Later had hij wel spijt van zijn kosmologische constante, en keerde hij terug naar zijn oorspronkelijke formule. Maar voor zover ik weet is hij nooit van gedacht veranderd over het oeratoom. En gedurende tientallen jaren dachten veel vakgenoten zoals Einstein in zijn eerste reactie: zelfs na een juiste berekening, als het resultaat niet geloofwaardig is, geloof het dan niet.
Er bestaat een ander model voor een uitdijend heelal. In de jaren 1940 stelde de Britse astrofysicus Fred Hoyle een model voor van een "steady state" (aanhoudende toestand) waarin hij veronderstelde dat terwijl de melkwegen uiteengaan, de achterblijvende lege ruimte nieuwe materie voortbrengt, zodanig dat de dichtheid en het algemene uitzicht van het heelal altijd gelijk blijven. In een radiouitzending in 1949 legde hij het verschil uit tussen de twee modellen: in zijn eigen model wordt het heelal voortdurend geschapen, en in het model van het kosmisch ei is de schepping plots gebeurd, met een grote knal. Dit beeld van de grote knal of oerknal was zo treffend, dat het de nieuwe naam werd van de theorie van Lemaître.
Maar in 1964 maakten Arno Penzias en Robert Woodrow Wilson, natuurkundigen in dienst van de Amerikaanse firma Bell, een kaart van de hemel met alle signalen die de communicatie met satelieten zouden kunnen verstoren. Ze stelden vast dat er een signaal is dat uit elke richting komt, zelfs uit delen van de ruimte waar niets te zien is. Ze zochten naar een verklaring voor dat signaal, en vonden een artikel terug uit 1948, waarin juist dergelijk signaal voorspeld werd als een restant van de oerknal. Na deze toevallige ontdekking van de kosmische achtergrondstraling, won het idee van de oerknal aanhangers. Het wordt nu algemeen aanvaard.
De kosmische achtergrondstraling is een overblijfsel van wat men soms de laatste fase van de oerknal noemt: de tijd waarin het heelal doorzichtig werd. Daarvoor bestonden er nog geen atomen, alleen vrije elektronen en atoomkernen. Die vrije elektrische ladingen zonden voortdurend lichtstralen uit, en vingen ze ook weer op. Lichtstralen bleven maar kort bestaan. Maar toen het heelal genoeg afgekoeld was, konden er zich atomen vormen, en werden vrije elektrische ladingen zeldzaam. Lichtstralen konden grote afstanden afleggen, miljarden lichtjaren, totdat ze opgevangen werden in de antenne van Penzias en Wilson.
Over de geschiedenis van het heelal sinds de oerknal weet men al enkele zaken, met meer of minder zekerheid, maar er blijven nog veel vragen. Het meest raadselachtige aan de oerknal is het begin ervan. Daar komt relativiteit in botsing met kwantumfysica.
Relativiteit, of de theorie van Newton als haar vereenvoudigde vorm, wordt gebruikt voor alles wat verband houdt met zwaartekracht, voor de beweging van vloeistoffen en gassen, en voor alle mechanische systemen, ook elektrische en brandstofmotoren. In dit deel van de wereld is ze met grote nauwkeurigheid juist.
Maar even juist, alleen op een ander terrein, is de kwantummechanica. Deze wordt vooral gebruikt waar de afstanden klein zijn; in molecules, atomen, en atoomkernen. Heel de scheikunde is af te leiden uit de kwantummechanica, maar ook transistoren, lasers, en fotoelektrische cellen. De kwantumtheorie behandelt goed de elektromagnetische kracht en twee soorten van kernkracht. Ze is combineerbaar met de speciale relativiteit, bijvoorbeeld om te berekenen hoe de massa van een elektron afhangt van zijn snelheid. Maar ze werkt niet in een ruimtetijd waarvan de kromming afhangt van wat erin gebeurt, en ze kent geen zwaartekracht. In een atoom heeft dat geen belang: waarschijnlijk beïnvloeden elektronen en protonen elkaar wel met hun zwaartekracht, maar de elektromagnetische wisselwerking is veel en veel groter.
In de eerste microseconde van de oerknal zijn beide theorieën belangrijk. De afstanden zijn zo klein, dat we kwantumeffecten niet kunnen verwaarlozen. Maar wegens de grote massadichtheid, geldt hetzelfde voor de algemene relativiteit. Er is een nieuwe theorie nodig die beide theorieën kan vervangen. Die theorie heeft al een naam: kwantumzwaartekracht. Maar ze is nog niet uitgevonden.
Maar misschien interesseert het u meer om te weten wat er voor de oerknal gebeurd is. Daar bestaan veel verhalen over, omdat tijdens de oerknal de nu nog onbekende kwantumzwaartekracht heerste, en alle overblijfselen van vroeger tijdens die periode op een onbegrepen manier vervormd moeten zijn.
Ik zal mij beperken tot een verhaal, het verhaal dat men het meest hoort, omdat het rechtstreeks volgt uit de berekening van Lemaître. Die berekening, die enkel steunt op relativiteit, verlengt geodetische lijnen. Dat kan, omdat de ruimtetijd glad is in alle eventen. Hieruit blijkt dat alle levenslijnen van de gekende wereld voortkomen uit een event waar de ruimtetijd oneindig dicht was. Oneindig dicht betekent oneindig krom, dus helemaal niet glad. Voorbij dit event is het niet mogelijk de lijnen te verlengen. Er bestaat geen vroeger. Wat is er daarvoor gebeurd? In een onbestaande tijd is niets gebeurd.
Datum waarop deze pagina laatst werd bijgewerkt: 2023-03-10