En 1931 profesoro Georges Lemaître de la universitato de Loveno proponis la ideon ke iam, inter 5 kaj 20 miliardoj da jaroj antaŭ nun, la universo komenciĝis kiel praatomo kun senfine densa maso. Tiu ideo nun estas ĝenerale akceptita, oni nomas ĝin praeksplodo, kaj situas ĝin antaŭ 13,7 miliardoj da jaroj.
La urbo Leuven ne volas atendi la 100-an jaron post tiu anonco por festi ĝin. Jam en 2021 ni festos la 90-jariĝon de la praeksplodo per granda kultura knalo. Kaj je tiu okazo, mi volas rakonti kial kaj kiel sciencistoj venis al tiu ideo.
Mi komencos la rakonton ĉirkaŭ la jaro 300 antaŭ Kristo.
En tiu tempo, la greka matematikisto Eŭklido de Aleksandrio kunigis la tiamajn konojn pri geometrio en libro, kiu dum jarmiloj estis modela por matematikistoj. Ĝi komenciĝis per kelkaj difinoj: pri tio mi parolos. Poste venis limigita nombro da bazaj asertoj: tion oni simple akceptu. Kaj fine venis nelimigita nombro da teoremoj (ĉiu rajtas aldoni siajn), pri kiuj oni pruvas ke ili estas logikaj sekvoj de la difinoj kaj bazaj asertoj.
Sed kiel dirite, la libro ne temis pri matematiko, sed pri geometrio: pri la spaco en kiu ni vivas, pri la formoj kaj grandoj en tiu spaco. Tio apartenas al fiziko. En fiziko oni ofte uzas matematikajn metodojn.
Ke Eŭklido ne pensis skribi pri pura matematiko, ni povas konkludi el la distingo kiun li faris inter siaj bazaj asertoj. En matematiko, baza aserto estas baza aserto. Aksiomo oni nomas ĝin. Eŭklido donis kelkajn aksiomojn, kiuj laŭ li estas evidentaĵoj. Tra du malsamaj punktoj iras unu kaj nur unu rekto. Ĉiuj konsentos pri tio. Sed aliflanke, li proponis unu postulaton, laŭ li aserto verŝajne vera, sed pri kiu oni povas dubi. Tra punkto ekster rekto iras en la sama ebeno, unu kaj nur unu paralela rekto. Ni supozu tion, kaj vidu al kio tio kondukos nin.
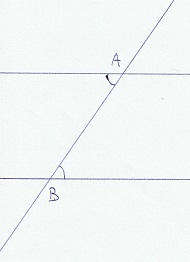Ni desegnu du paralelajn rektojn, kaj tra ili tria rekto. Ni tuj vidas ke la
anguloj en A egalas al la anguloj en B. La malgranda angulo en A ne povas esti pli granda nek pli malgranda ol tiu en B, ĉar la du punktoj troviĝas en
la sama pozicio rilate unu al la alia, kaj la paraleloj estas unikaj.
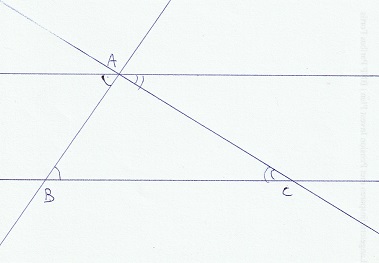Se ni nun aldonas plian rekton tra A, la indikitaj anguloj en A kaj C
kompreneble ankaŭ estas egalaj. Sub la punkto A, ni nun vidas ke la sumo de la anguloj de triangulo estas egala al 180°.
El tio sekvas ke ekzistas egalformaj trianguloj kiuj ne necese estas same grandaj: simple kopiu du angulojn de la unua triangulo (la distanco ne gravas), kaj la tria angulo de la nova triangulo aŭtomate egalos al la tria angulo de la unua.
El la proprietoj de samformaj trianguloj sekvas preskaŭ la tuta eŭklida geometrio: ĉio kio koncernas longojn. La postulato de Eŭklido estas tre grava
por koni la spacon en kiu ni vivas.
Sed ni facile povas imagi, eble ne en tri dimensioj, sed en du, alian mondon. Imagu dudimensiajn estaĵojn, vivantaj en sfera surfaco. Sur sfero ĉiu triangulo sumiĝas al pli ol 180°. Sed niaj dudimensiuloj konas nur malgrandan parton de sia mondo: ili konas Lovenon sur la tera surfaco. En Loveno la sumo de triangulo estas 180°, fakte iomete pli, sed la diferenco estas nemezureble malgranda. La mondo ŝajnas eŭklida.
Jen vera scienco: eble ne tute vera, neniam tute certa, sed ja precize ĝusta en la parto de la mondo kiun ni konas.
En la 16-a kaj 17-a jarcentoj pluraj sciencistoj pristudis movadojn. Johannes Kepler priskribis la movadon de la planedoj. Galileo Galilei pristudis movadojn sur la tero kaj la influon de gravito. Isaac Newton resumis la rezultojn de Galileo en pli matematika sistemo, kaj eksplikis la leĝojn de Kepler pri la planeda movado per la sama gravito kiun Galileo priskribis sur la tero.
Du ideoj el tiu tempo gravas por mia rakonto.
Ja kelkaj observantoj estas specialaj: la inerciaj observantoj, tiuj sur kiuj agas neniu neta forto. Rilate unu al la alia, inerciaj observantoj aŭ ne moviĝas, aŭ moviĝas laŭ rekta linio kun konstanta rapido.
Ke tiuj du masoj estas aspektoj de la sama realo, li deduktis el pluraj faktoj, sed ĉefe el eksperimento de Galileo, kiu faligis du kuglojn, unu el plumbo, la alia el fero, el alta turo. La kugloj samtempe atingis la teron. Tiu eksperimento poste estis ofte ripetita kun objektoj el diversaj materialoj kaj kun diversaj formoj, eĉ kun plumo kaj kuglo en vakua tubo, kaj ĉiam kun la sama rezulto.
En la 19-a jarcento Michael Faraday eksperimentis pri elektro kaj magnetismo kaj la interagoj inter ambaŭ. James Clerk Maxwell konstruis el liaj rezultoj la teorion de elektromagnetismo. El tiu teorio sekvis ke devas ekzisti elektromagnetaj ondoj, kiuj propagiĝas tra vakuo kun konstanta rapido kalkulebla el la rezultoj de Faraday. Tiu rapido egalas al la tiam jam mezurita rapido de lumo. Pro tio, oni tuj supozis, kaj poste pruvis, ke lumo estas elektromagneta ondo.
Sed ondo tra vakuo, ĉu tio havas rapidon? Rilate al kio? Rilate al la instrumentoj de Faraday en Londono ne ŝajnas kredinda respondo. La unua ideo estis ke la ondoj trairas eteron, speciala substanco kiu ne interagas kun alia materio, sed kies sola funkcio estas subteni la lumajn ondojn.
Bone. Sed tiu etero ja devas havi lokon. Verŝajne, ĉar la tero ĉirkaŭiras la sunon kun rapido de 30 km/s, la tero devas moviĝi rilate al la etero. Lumo iranta en la sama direkto kiel la tero devas esti malpli rapida rilate al la tero ol lumo en la kontraŭa direkto. Sed eksperimentoj ne trovis diferencon.
En 1905 Albert Einstein proponis solvon sen etero. Ni simple akceptu ke la lumrapido estas la sama por ĉiu observanto: ni ŝanĝu la relativecteorion de Galileo.
 |
 |
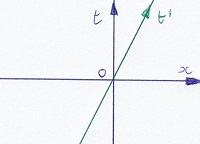
Konsideru ĉi tiun diagramon. Horizontale mi metas la spacon, vertikale la tempon. De la spaco mi desegnas nur la koordinaton x, sed ĉiuj konsiderataj movadoj okazos en pozitiva aŭ negativa x-direkto. Punktoj en tia diagramo estas nomataj eventoj, ĉar ili indikas kaj lokon kaj tempon. La evento O estas la referenco: tie x kaj t estas nulaj. La diagramo montras la eventojn el la vidpunkto de firma tero. En la evento O, trajno preteriras je konstanta rapido. La verda linio montras eventojn ligitajn al loko en la trajno.
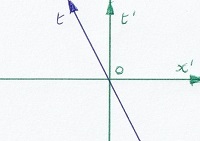
Sube, mi desegnas la samajn eventojn el la vidpunkto de la trajno. En ambaŭ desegnoj, vertikalaj linioj montras samlokajn eventojn. En la unua desegno, la punkto en la trajno iras dekstren, en la dua, la sama punkto ne moviĝas, sed la firma tero iras maldekstren.
Galileo diras nenion pri la tempo, sed implice li supozas ke la tempo estas sama por ĉiuj. Horizontalaj linioj en la diagramo restas horizontalaj.
 |
 |
Sed kun konstanta lumrapido tio ne eblas. Mi aldonu ruĝe du lumradiojn tra O: unu en pozitiva, la alia en negativa x-direkto. La unuojn de longo kaj de tempo mi elektis tiel, ke la rapido de lumo estu unu: unu lumsekundo en sekundo. Vi vidas ke nia trajno estas tre rapida. Por malpli rapida trajno la teorio de Einstein ŝanĝus preskaŭ nenion.
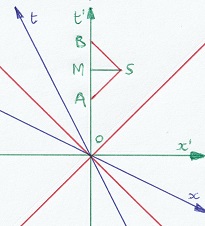
Kio ŝanĝiĝas? En la trajno (suba desegno), en la evento A, oni sendas lumradion al spegulo. En la envento B ĝi revenas. La spegulo troviĝas sur la trajno, do la distanco al ĝi ne ŝanĝiĝas. La evento de spegulado S estas samtempa kun M, meze inter A kaj B.
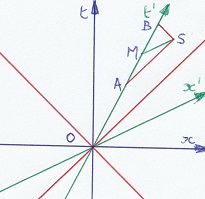
Ni desegnu (supre) la samajn eventojn el la vidpunkto de la firma tero. A kaj B troviĝas sur la linio kiu reprezentas la movadon de la trajno. M troviĝas meze inter ili. La lumo havas konstantan rapidon, do ni povas desegni kiel ĝi foriras, kaj kiel ĝi revenas. La evento S estas kie la du lumradioj renkontiĝas. El la vidpunkto de la trajno S estis samtempa kun M. Sed el la vidpunkto de la firma tero tiuj eventoj ne estas samtempaj: samtempaj eventoj por unu observanto ne estas samtempaj por la alia. Kiel la loko estas relativa, tiel ankaŭ la tempo.
Ni supozu ke t estas mezurita en la samaj unuoj kiel la spacaj koordinatoj x, y kaj z, tiel ke la rapido de lumo estu 1. Oni povas pruvi ke por ajna
evento P (x, y, z, t) la kalkulo x2 + y2 + z2 - t2 donas la saman rezulton por
ambaŭ observantoj. Oni nomas ĝin la intervalo inter O kaj P, evitante la vorton distanco, ĉar distanco inter malsamaj punktoj ne povas esti nula. Por
eventoj sur lumradio el O, la intervalo estas nula. Kiam ĝi estas pozitiva, ĝi estas la kvadrato de la propra distanco, la distanco kiun mezurus
observanto laŭ kiu la eventoj estas samtempaj. Se negativa, ĝi estas minus la kvadrato de la propra tempo, la tempodiferenco laŭ kunvojaĝanta
observanto.
Tiu formulo, kune kun kelkaj supozoj kies celo estas konservi ĉe malgrandaj rapidoj la jam konatajn leĝojn de la naturo, estas la bazo de kio nun estas nomata la Speciala Teorio de Relativeco, speciala ĉar ĝi konsideras nur la specialan kazon de observantoj kun konstanta rapido.
Mi ne detalos pri ĝi. Nur unu rezulton ni bezonos en la sekvo. Se la formulo de Newton en kiu aperas la inercia maso de objekto plu validu, tiu maso
devas dependi de la rapido de la objekto: ju pli granda la rapido, des pli granda la maso. La propra maso estas la maso mezurita de kunvojaĝanta
observanto. Lumo ne havas propran mason, ĉar ĝia rapido estas la sama por ĉiuj observantoj: ne ekzistas observanto por kiu ĝi estas nula. Kaj objekto
kies propra maso ne estas nula, ne povas plirapidiĝi ĝis la rapido de lumo, ĉar por tio necesus senfina forto.
La Ĝenerala Teorio de Relativeco, publikigita en 1916, estas pli komplika. Mi eksplikos ĝin, sed antaŭe mi diru ion pri aŭtomobiloj. Aŭtomobilo estas simpla objekto, kondiĉe ke oni ne rigardu la motoron, la stirilon kaj la pedalojn. La samo validas por Relativeco: mi eksplikos la kvar radojn.
La Speciala Relativeco diras nenion pri kion vidas observanto kies rapido ne estas konstanta. Aldone, ĝia apliko donis problemojn en gravita kampo.
Pripensante tiujn problemojn, Einstein rememoris la eksperimenton de Galileo kun la falantaj objektoj. Du objektoj en libera falo en gravita kampo ne moviĝas rilate unu al la alia. Ĉu ni ne supozu ke ĝuste libere falanta objekto estas la inercia observanto por kiu validas la supozoj de Speciala Relativeco? Ni supozu spacotempon kurbigitan de la gravito tiamaniere, ke libere falantaj objektoj el sia propra vidpunkto sentu neniun forton, kaj najbaraj falantaj objektoj el tiu vidpunkto moviĝu laŭ rekta linio.
La solvo de la problemo kuŝis do en kurba geometrio, kiel la ne-eŭklidaj geometrioj kiujn Bernard Riemann pristudis matematike komence de la 19-a jarcento. La geometrio de Ĝenerala Relativeco estas nomata pseŭdo-riemanna, pro la speciala distancoformulo kun pozitivaj kaj negativaj intervaloj, sed plej multaj teĥnikoj de Riemann restas uzeblaj en ĝi.
Dudimensian spacon de Riemann ni povas facile imagi. Pensu pri la surfaco de montara pejzaĝo, kun montoj kaj valoj, grotoj kaj elstaraĵoj, sed ja glata en ĉiu punkto. Tio signifas ke ĉirkaŭ ĉiu punkto ekzistas ĉirkaŭaĵo tre simila al eŭklida ebeno: kun rektaj linietoj, trianguloj de 180°, kaj la konataj distancoj inter najbaraj punktoj. Nur se oni konsideras pli grandan ĉirkaŭaĵon, oni eble konstatos ke la spaco estas kurbita: la sumo de la anguloj de granda triangulo ne estas ekzakte 180°, sed iomete pli (kiel sur sfero) aŭ malpli (kiel sur sela surfaco).
Rektoj ne ekzistas en tia spaco, almenaŭ oni ne parolas pri rektoj. Laŭ Eŭklido, rekto estas determinita per du ĝiaj punktoj. Tra du malsamaj punktoj iras unu kaj nur unu rekto. Tiaj rektoj ne ekzistas. Ja ekzistas geodeziaj linioj: linioj kiuj estas rektaj en la eŭklida ĉirkaŭaĵo de ĉiu punkto. El ĉiu punkto, la linio iras rekte al najbara punkto, de la najbaro ĝi rekte pluiras al aliaflanka najbaro, kaj tiel plu.
 |
 |
Geodezia linio estas la plej mallonga vojo inter du ĝiaj punktoj, en tiu senco ke malgranda ŝanĝo al la linio povas nur plilongigi ĝin. Sed ja eblas ke tute alia geodezia linio, kun malsama longo, iru tra la samaj du punktoj.
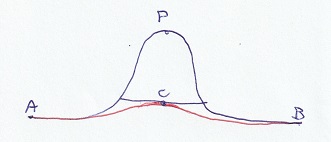
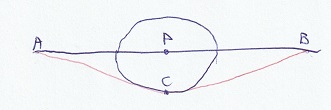
Prenu ĉi tiun monton. Mi desegnis la samajn punktojn kaj liniojn dufoje, el malsamaj vidpunktoj. Supre vi vidas ke temas pri monto, sube ke la monto estas ronda. La plej mallonga vojo de A al P kaj la plej mallonga vojo de P al B ambaŭ estas geodeziaj. En la punkto P ili plilongigas unu la alian. Tial la tuta vojo de A al B tra P estas geodezia. Sed alia geodezia vojo, tra C, estas pli mallonga.
Tian spacon, sed kvardimensian kun speciala statuto por la tempo, proponis Einstein en sia teorio de Ĝenerala Relativeco. Ĉeestantaj masoj determinas la formon de la spaco, kaj falanta objekto moviĝas tra tiu kurbita spaco laŭ geodezia trajekto.
Estas iom pli komplike. En Speciala Relativeco, la maso de objekto dependas de ĝia rapido. Malsamaj observantoj vidas malsaman mason. Oni ja povas
reprezenti la mason de rektlinie moviĝanta objekto per vektoro. Vektoro estas matematika objekto kiu reprezentas realaĵon kiun malsamaj observantoj
priskribos per malsamaj mezuroj. Ekzemple rapido de movado en tridimensia spaco: oni havas rapidon en x-direkto, en y-direkto kaj en z-direkto. Elektu
aliajn x, y kaj z, kaj la tri nombroj ŝanĝigos, por priskribi la saman movadon. En speciala relativeco, la kvardimensia vektoro kiu anstataŭas la mason
konsistas el la maso vidita de observanto (multiplikita per la lumrapido) kaj la movokvantoj (maso foje rapido) en la tri spacaj direktoj.
En kurbita spacotempo, eĉ tio ne eblas, ĉar punktoj de la sama objekto ne havas la saman rapidon rilate al la observanto. Pensu nur pri turniĝanta rado. Kiel oni difinu la mason de tia objekto? Oni ja povas paroli pri unuopaj punktoj de la objekto, kaj priskribi la lokan mason per tensoro, speco de ĝeneraligita vektoro, kies mezuroj dependas de pli ol unu direkto. Tiu tensoro ekzistas en ĉiu evento, kaj determinas por ĉiu observanto kelkajn grandojn, kiujn mi donas en vicordo de graveco, supozante ke la rapidoj estas malgrandaj.
Tiu tensoro de denseco, fluo kaj streĉo determinas la lokan kurbitecon de la spaco, en tia maniero ke ĉe malgrandaj rapidoj oni retrovu la movadojn kiujn antaŭdiras la leĝoj de Newton.
Bela rezulto, ĉu ne? Per kalkulo pli komplika ol tiu de Newton, ni trovas la samajn rezultojn. Sed la kalkulo de Newton validas nur ĉe malgrandaj rapidoj kaj streĉoj. Astronomoj jam de longe serĉis eksplikon por strangaĵo en la orbito de Merkuro. Planedoj influas unu la alian. Tio komplikigas iliajn orbitojn, sed detala kalkulo de planedaj orbitoj ĝenerale donis la observitajn movadojn. Nur ĉe Merkuro restis neregulaĵo neeksplikita, pli granda ol la necerteco pri la observoj. Merkuro estas la planedo plej proksima de la suno. Pro tio, ĝi ankaŭ estas la plej rapida planedo, por kiu la diferenco inter Newton kaj Einstein estas plej granda. La kalkulo de Einstein pri Merkuro donis preskaŭ ekzakte tion, kion serĉis la astronomoj.
Einstein eksplikis observojn jam faritajn, sed li ankaŭ antaŭdiris novan observon. Se gravito determinas la formon de la spacotempo, tio influas ne nur planedojn, sed ankaŭ la lumon. Ankaŭ lumo devas sekvi geodezian vojon, ĉar rekta vojo ne ekzistas. Lumo kiu preteriras proksime de la suno devas, el nia vidpunkto, esti devojigita. Steloj kies nokta pozicio sur la ĉielo estas bone konata, devas havi iom alian pozicion kiam la suno ŝajnas apuda. Oni neniam rimarkis tion, ĉar stelojn oni rigardas nur nokte. Tage tio eblas nur dum suna eklipso. Dum eklipso en 1919 oni rigardis la stelojn, kaj trovis ilin en la lokoj kalkulitaj de Einstein.
Newton jam konsideris jenan demandon: se la gravito estas universala, ankaŭ steloj devas altiri unu la alian. Ĉu la universo ne devas ŝrumpi? Lia respondo estis, ke en senfina universo tio ne estas problemo: la suno estas tirata tien kaj tien kaj tien, sed la kuna efiko de tiuj kontraŭaj fortoj estas nula: la suno ne moviĝos, nek la aliaj steloj.
|
Fakte, estas la rusa fizikisto Aleksandr Fridman kiu atentigis Einstein pri tio en 1922. Sed ĉar li mortis en 1925, kaj liaj artikoloj ĝis tiam ne altiris multan atenton ekster Sovetio, li ne ludos rolon en la sekvo. |
Einstein rekonsideris la demandon. En Ĝenerala Relativeco gravito ne estas forto, sed kurbiĝo de la spaco. Geodeziaj vivpadoj kiuj iumomente ŝajnis paralelaj, kiel meridianoj sur la ekvatoro, tamen povas kuniĝi poste. Objektoj kiuj ne moviĝas space, estonte kunvenos pro la kurbiĝo kiun ili kaŭzas en la spacotempo. La influo de malproksimaj objektoj ne ŝanĝos tion. Nemoviĝanta universo ŝrumpos, ĉu ĝi estu senfina, ĉu ne. La diferenco estas, ke en la mondo de Newton, ŝrumpado de la universo eblas nur se ĉiuj steloj moviĝas al unu centra punkto. Senfina universo ne havas centron, kaj ne povas ŝrumpi. En la mondo de Einstein, centra punkto ne estas bezonata. El sia propra vidpunkto ĉiu stelo povas resti surloke, sed la aliaj proksimiĝos.
Se la universo jam estas ekspansianta, tiu ekspansio pludaŭros ankoraŭ iomete. Ĉu ĝi daŭros eterne, dependas de la nunaj rapido de la ekspansio kaj masodenseco de la universo. Sed ĉar en tiu tempo, komence de la dudeka jarcento, astronomoj ĝenerale pensis ke la denseco de la universo ne ŝanĝiĝas, Einstein adaptis sian originalan formulon de Ĝenerala Relativeco, enkondukante ankoraŭ nekonatan kosmologian konstanton. Tiu konstanto devis efiki kiel negativa kurbiĝo de malplena spaco. Masoj altiras unu la alian, sed se ilia distanco estas sufiĉe granda, la malplena spaco inter ili forpuŝas ilin.
Sed ankaŭ la astronomia scienco pluevoluis.
En la deknaŭa jarcento oni jam mezuris multajn ĉielajn distancojn per komparo de perspektivoj. Por planedoj oni komparis observojn el malsamaj observatorioj. Por steloj oni uzis fotojn faritajn per la sama teleskopo, sed el malsamaj pozicioj de la tero en sia orbito ĉirkaŭ la suno. Tiel oni jam konis la distancojn al multaj najbaraj steloj.
En la dudeka jarcento oni komencis uzi biologian metodon por almenaŭ havi ideon pri pli longaj distancoj. Kiam biologo vidas elefanton, li tuj rekonas ĝian formon, kaj el la ŝajna grando de la besto li povas dedukti la distancon. Kiam li rekonas muŝon, li atribuos al ĝi alian distancon. Ankaŭ inter la steloj troviĝas tiaj "bestoj" kies grando estas konata de astronomoj. Tiel oni sukcesis pruvi ke pluraj tiel nomataj nebulozoj estas multe pli malproksimaj ol la konataj steloj, kaj ke ili mem estas stelaroj kompareblaj al la Lakta Vojo. Oni nun nomas ilin galaksioj, laŭ la greka nomo de la Lakto Vojo. Similsona vorto estas uzata en pluraj lingvoj, sed en la nederlanda oni simple parolas pri laktaj vojoj.
En la 1920-aj jaroj, Edwin Hubble mezuris la distancojn kaj ruĝenŝovojn de dudeko da galaksioj. La ruĝenŝovo estas proprieto de la spektro de lumo. La lumo de steloj kaj galaksioj, kiam oni separas ĝiajn kolorojn, montras rekoneblan patronon, sed tiu patrono povas esti ŝovita al pli grandaj aŭ pli malgrandaj frekvencoj depende de la movado de la stelo rilate al ni. Ŝovo al la blua (pli grandaj frekvencoj) signifas ke la stelo alproksimiĝas. Sed preskaŭ ĉiuj galaksioj foriras de ni: ilia spektro havas pozitivan ruĝenŝovon. Hubble trovis ke ju pli malproksima la galaksio, des pli granda ĝia ruĝenŝovo.
Kvankam Hubble faris tiujn observojn, estas Lemaître kiu kiel unua publikigis la konkludon, ĉar pro teoriaj konsideroj li sentis sin sufiĉe certa por fari tion. Kalkulo per Ĝenerala Relativeco lernis al li ke se la universo estas ekspansianta nun, ĝi devas esti ekspansiinta antaŭe, kaj la komenco de tiu ekspansio devas esti evento kun senfina denseco, okazinta en finia tempo antaŭ nun. Tio validas por ĉiu ebla valoro de la kosmologia konstanto.
Kiam Lemaître parolis al Einstein pri tiu teorio de la senfine densa praatomo (poste li nomos ĝin kosma ovo), Einstein tuj respondis "Viaj kalkuloj estas ĝustaj, sed via fiziko estas abomeninda." Poste li tamen bedaŭris la enkondukon de la kosmologia konstanto, kaj revenis al la pli simpla originala formulo. Sed laŭ mia scio li neniam ŝanĝis sian opinion pri la praatomo. Kaj dum jardekoj plej multaj fakuloj pensis kiel Einstein en sia unua reago: eĉ post bona kalkulo, se la rezulto ne estas kredinda, ne kredu ĝin.
Ekzistas alia modelo de ekspansianta universo. En la 1940-aj jaroj, la brita astrofizikisto Fred Hoyle proponis modelon de "konstanta stato" kiu supozis ke dum la galaksioj foriras, la postlasita malplena spaco naskas novan materion, tiel ke la denseco kaj la ĝenerala aspekto de la universo ĉiam restos la samaj. En radioelsendo en 1949 li klarigis la diferencon inter la du modeloj, dirante ke en lia modelo la universo daŭre estas kreata, kaj en la modelo de la kosma ovo ĝi estas kreita subite, per granda knalo. Tiu bildo de granda knalo aŭ praeksplodo estis tiom trafa, ke ĝi iĝis la nova nomo de la teorio de Lemaître.
Sed en 1964, Arno Penzias kaj Robert Woodrow Wilson, fizikistoj kiuj laboris por la usona kompanio Bell, faris mapon de la ĉielo kun ĉiuj signaloj kiuj povus perturbi la komunikadon kun satelitoj. Ili konstatis ke el ĉiu direkto venas signalo, eĉ el regionoj en la spaco kie nenio estas videbla. Serĉante klarigon por tiu signalo, ili trovis artikolon el 1948, en kiu ĝuste tia signalo estis antaŭdirita kiel restaĵo de la praeksplodo. Post tiu hazarda malkovro de la kosma fona radiado, la ideo de praeksplodo iom post iom gajnis terenon. Ĝi nun estas ĝenerale akceptita.
La kosma fona radiado estas restaĵo de tio kion oni ofte indikas kiel la lasta fazo de la praeksplodo: la tempo kiam la universo iĝis travidebla. Antaŭe ne ekzistis atomoj: nur liberaj elektronoj kaj atomaj nukleoj. Tiuj liberaj elektraj ŝargoj senĉese elsendis kaj reabsorbis lumradiojn. La ekzisto de lumradioj estis mallongdaŭra. Sed kiam la universo estis sufiĉe malvarmiĝinta, atomoj povis formiĝi, kaj liberaj elektraj ŝargoj iĝis maloftaj. Lumradioj povis trairi grandajn distancojn, miliardojn da lumjaroj, antaŭ ol esti kaptitaj de la anteno de Penzias kaj Wilson.
Pri la historio de la universo ekde la praeksplodo oni jam scias kelkaj aferojn, kun pli aŭ malpli granda certeco, sed restas multaj demandoj. La plej granda mistero de la praeksplodo estas ĝia komenco. Tie relativeco konfliktas kun kvantumfiziko.
Relativeco, aŭ la teorio de Newton kiel ĝia simpligita versio, estas uzata por ĉio kio rilatas al gravito, por la movadoj de likvoj kaj gasoj, kaj por ĉiuj meĥanikaj sistemoj inkluzive de elektraj kaj brulaĵaj motoroj. En tiu parto de la mondo ĝi estas tre precize ĝusta.
Sed egale ĝusta, nur en alia tereno, estas kvantummeĥaniko. Tiun oni uzas ĉefe kie distancoj estas malgrandaj: en molekuloj, atomoj, kaj atomaj nukleoj. La tuta ĥemio estas derivebla de kvantummeĥaniko, sed ankaŭ transistoroj, laseroj, kaj lumelektraj ĉeloj. Kvantuma teorio bone pritraktas la elektromagnetan forton kaj du specojn de nuklea forto. Ĝi estas kombinebla kun speciala relativeco, ekzemple por kalkuli kiel la maso de elektrono dependas de ĝia rapido. Sed ĝi ne funkcias en spacotempo kies kurbiteco dependas de la movadoj en ĝi, kaj ne konas graviton. En atomo tio ne gravas: elekronoj kaj protonoj verŝajne ja interagas per gravito, sed la elektromagneta interago estas multe pli forta.
En la unua mikrosekundo de la praeksplodo, ambaŭ teorioj gravas. La distancoj estas tiel malgrandaj, ke oni ne povas neglekti kvantumajn efikojn. Sed pro la granda masodenseco, la samo validas por ĝenerala relativeco. Oni bezonas novan teorion, kiu anstataŭu kaj kvantummeĥanikon, kaj ĝeneralan relativecon. Tiu teorio jam havas nomon: kvantumgravito. Sed ĝi ankoraŭ ne estas inventita.
Sed eble vin pli interesas la demando, kio okazis antaŭ la praeksplodo. Ekzistas multaj rakontoj pri tio, ĉar dum la praeksplodo regis la ankoraŭ nekonata kvantumgravito, kaj ĉiuj indikoj pri pli fora pasinto estis transformitaj dum tiu mistera periodo.
Mi limigos min al unu rakonto, la rakonto kiun oni plej ofte aŭdas, ĉar ĝi plej rekte sekvas el la kalkulo de Lemaître. Tiu kalkulo, pure relativeca, plilongigas geodeziajn liniojn. Tio eblas, ĉar la spacotempo estas glata en ĉiu evento. La konkludo estas ke ĉiuj vivlinioj de la konata mondo fontas el unu evento kie la spacotempo estis senfine densa. Senfine densa signifas senfine kurbita, do tute ne glata. Tra tiu evento oni ne povas plilongigi liniojn. Pli frue ne ekzistas. Kio okazis antaŭe? En neekzistanta tempo okazis nenio.
Dato en kiu tiu ĉi paĝo estis lastfoje aktualigita: 2021-03-10